Using SVG with CSS3 and HTML5 — Supplementary Material

Example code and online extras for the O'Reilly Media book by Amelia Bellamy-Royds, Kurt Cagle, and Dudley Storey.

Chapter 11
Transformative Changes: Coordinate System Transformations

This chapter introduces the SVG transform attribute, and examines the ways in which you can work with the SVG coordinate system to make the most of transformations.

Like the nested coordinate systems created with <svg> and <symbol>, transformations allow you to reposition your origin or change the scale of your units. But transformations don’t stop there.

Transformations can change the definition of what “horizontal” or “vertical” means. This means you can draw rectangles and ellipses that don’t align with the browser window, without having to use <path> notation and trigonometry.

Furthermore, while new coordinate systems must be defined with a separate <svg> or <symbol> element, a transform can be applied directly—as an attribute—on individual shapes or on groups. This makes transformations incredibly flexible, and they are widely used in SVG.

Since transformations control the geometry of your drawing, transform was originally defined as a core XML attribute. However, transformations are so useful that web designers wanted to use them for non-SVG content. The CSS Transforms module defines how transformations can be set using CSS style rules, for any content controlled by CSS.

Figures and Examples#

The file names link to the code view on GitHub. Beware: the linked screenshots are hi-resolution; some have very large file sizes.

View all files for this chapter on GitHub.

Figure 11-1. A heart icon at many scales
Example 11-1. Scaling an icon with <symbol> and <use>
Example 11-2. Scaling an icon with transformations
Figure 11-2. Scaling a heart icon within a centered coordinate system
Example 11-3. Centering an icon within the coordinate system to control the scaling origin
Figure 11-3. Stroked circles at various scales
Example 11-4. Scaling a stroked shape
Another example of non-uniform scales (which was cut from the book)
Figure 11-4. Mirrored text created with negative scaling factors
Example 11-5. Using negative scaling factors to create reflections of text
Figure 11-5. A forest pattern created with translated club icons
Example 11-6. Using translations to position a repeated icon
Figure 11-6. Scaling a heart icon after centering it with translations
Example 11-7. Using translations to center a coordinate system for scaling
Figure 11-7. A wreath of icons created with rotations
Example 11-8. Rotating a graphic around the origin
Figure 11-8. A complex pattern created by rotating a single icon around two centers
Example 11-9. Rotations around arbitrary points
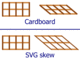Figure 11-9. Understanding skew: flattening a cardboard grid versus skewing an SVG grid
Figure 11-10 and 11-X2. A pseudo-3D drawing of a box built from skewed rectangles
Example 11-10. Using skew transformations to simulate three dimensions
Figure 11-11. Text with a projected shadow created with skew transformations
Example 11-11. Creating a projected shadow effect with skew transformations
Figure 11-12. An SVG face, and the same drawing with a matrix transformation applied
Figure 11-X1. A schematic for determining the direction of the z axis in a left-handed coordinate system
Figure 11-X3. A 3D “box”, when each side is flattened onto a canvas before the canvas is tilted towards the viewer
Example 11-X1. Using 3D transformations to build a box in preserve-3d space
Figure 11-X4. A 3D box, tilted towards a viewer at an infinite perspective distance
Example 11-X2. Using 3D transformations to build a box in preserve-3d space
Figure 11-X5. A 3D box, viewed from above and to the side (as rendered in Firefox 54)
Example 11-X3. Using 3D transformations to build a box, and 3D perspective to display it
Figure 11-X6. A 3D box, viewed from above and to the side, as rendered in Firefox 54 after changing the viewBox scale to match the display scale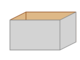
Figure 11-X7. A 3D box, viewed from above and to the side, as rendered in Chrome 57 after converting perspective effects into transform function lists
Example 11-X4. Integrating 3D perspective effects in an individual element’s transformation sequence
Figure 11-X8. Text that casts a shadow in three dimensions
Figure 11-X9. Text that casts a shadow in three dimensions, in a different browser
Example 11-X5. Using 3D transformations to cast a shadow

Online Extras#